The famed physicist Richard Feynman once said, “I learned very early the difference between knowing the name of something and knowing something,” a lesson from his father. I think too often we in the statistics/machine learning field are guilty of “only knowing the name of something.” Well, in most cases, we may know a bit more than the name, but not as much as we should to be able to use the concept usefully.
As in most of my stat posts, I hope there is something here for everyone. Some of this will be new and thought provoking for those who are already familiar with causal analysis, but also useful as an introduction for those who don’t have such background.
The post is aimed at developing insight beyond “the name of something” in causal analysis (CA), a data science topic that is not new but has become much more prominent in recent years. As you will see, I am something of a skeptic on CA, and hope to dispel some common misunderstandings regarding it. Make no mistake–I do believe CA is a useful tool–but I hope here to demystify some of the ideas, and bring it down to Earth in terms of the extent of its value.
We will begin by dispelling a common myth about regression analysis (not solely about causal analysis, just ordinary stat, but strongly related). This is such a common myth that some readers will have trouble fully accepting it. How is that for a tantalizing lure?
A quick bit of notation:
Let m(t) = E(Y|X=t) denote the conditional mean of Y given X = t. This is the regression function of Y on X, a function of t in our notation here. X is a vector of predictors/features. If say X is height and Y is weight, then m(70) is the mean (population) weight among people of height 70. If X is height and age, m(70,28) is the mean weight among people of height 70 and age 28. Note that we are not necessarily assuming a linear model for m(t) here, though we often will.
Dispelling a very common myth:
It will be absolutely crucial here to have a firm understanding of what a regression model really does.
One often hears statements like, “We’d like to use a regression model to investigate the impact of family income on such-and-such, but our data is skewed toward the middle class or higher, so our estimated coefficients will be skewed as well.”
For instance, is a student’s performance on the SAT related to family income? We might try to investigate that by fitting a linear model in which we predict SAT by high school grades HGPA and family income FI. The coefficient of FI might give us an idea of how much, if any, income affects SAT scores.
But if in our dataset FI is skewed toward the higher incomes, many people would say such an analysis is invalid.
Actually, there is no validity problem. Let’s take a look at some simulated data.
m <- matrix(rnorm(10000*2),ncol=2)
x <- m[,1]
y <- m[,1] + m[,2]
coef(lm(y ~ x))
# (Intercept) x
# 0.002190729 1.003438820
y <- y + 2
x <- x + 2
coef(lm(y ~ x))
# (Intercept) x
# -0.004686912 1.003438820
What happened here? We simulated a simple example in which m(t) = t, and of course the estimated coefficients were close to 1 and 0. Then we skewed the data to the right, and sure enough, got essentially the same answer.
How about this?
m <- matrix(rnorm(10000*2),ncol=2)
x <- m[,1]
y <- m[,1] + m[,2]
whichBig <- which(x > 1.5)
x <- x[whichBig]
y <- y[whichBig]
coef(lm(y ~ x))
# (Intercept) x
# 0.2525674 0.8474718
m <- matrix(rnorm(100000*2),ncol=2)
x <- m[,1]
y <- m[,1] + m[,2]
whichBig <- which(x > 1.5)
x <- x[whichBig]
y <- y[whichBig]
coef(lm(y ~ x))
# (Intercept) x
# -0.06571407 1.04364323 Here we said, let’s look at only part of our data, the part in which X > 1. Do the estimated coefficients still come out to be about 1 and 0? Turned out not to be, but because I knew they “should” be about 1 and 0, I knew it was a sample size issue. I thus tried a much larger sample, and sure enough, we did indeed get approximately 1 and 0.
To be sure, if we fit a linear model, or logistic or other parametric model, the above points will depend on the model being correct (or nearly so; no parametric model is exact in practice). To eliminate this issue, let’s look at nonparametric methods, which are always correct. Let’s try k-Nearest Neighbors (kNN).
library(qeML)
data(svcensus)
names(svcensus)
# [1] "age" "educ" "occ" "wageinc" "wkswrkd" "gender"
median(svcensus$age)
# [1] 38.21515
# a young person for our 't'
t0 <- data.frame(age=28,educ='16',occ='102',wkswrkd=52,
gender='male')
# estimated m(t), using k-Nearest Neighbors
knnOut <- qeKNN(svcensus,'wageinc',holdout=NULL)
predict(knnOut,t0)
# [,1]
# [1,] 74068
# skew the data toward older
svc1 <- svcensus
which25plus <- which(svc1$age > 25)
svc1 <- svc1[which25plus,]
knnOut1 <- qeKNN(svc1,'wageinc',holdout=NULL)
predict(knnOut1,t0)
# [,1]
# [1,] 74068No change! The skewing had no effect.
What is going on here? Mathematically, if t is in A, then
E(Y | X = t, X in A) = E(Y | X = t)
since X = t is more restrictive than X in A.
Bottom line: The common thinking that “The distribution of X is skewed,” so this distorts our linear regression analysis,” is incorrect. True, as is always the case with linear models, one must check for linearity (see below), and pay attention to sample sizes (via a look at the size of the estimated coefficients’ standard errors), but there is nothing inherently distortionary about a skewed X distribution.
A specifically causal-analytic example of this idea:
Think of a university and its admissions policy, under which a student is admitted if either their SAT score or high school grade point average HGPA are above a certain threshold, s and h, respectively. Suppose we are interested in the individual effects of SAT and HGPA on university grade point average UGPA, and are considering using a linear model.
Causal analysis enthusiasts who are reading this would immediately recognize this situation as involving a collider. This is taken a danger signal, for a good reason in one particular sense to be described below, but on the other hand it does NOT invalidate our analysis of the individual effects of SAT and HGPA.
We are modeling E(UGPA | SAT=t1 and HGPA=t2), i.e. Y = UGPA and X = (X1,X2) = (SAT,HGPA). The structure of the admissions process is such that our data has been restricted to the set {X1 >= s or X2 >= h}. Due to the considerations discussed above, we see that this restriction does NOT change our estimate of m(t), i.e. our estimated regression coefficients in a linear model. Our ordinary linear model is still valid.
On the other hand, the situation is different if the object of our interest involves the distribution of X itself. For example, we may be interested in the correlation between X1 and X2 here. This should be substantially positive in the general population, but probably will be weaker in the subpopulation of those admitted to the university
Comparing classical and causal analyses:
Do coaching schools increase a student’s SAT test score? Much has been written on this issue pro and con, but here we will be interested less in the answer than the types of analysis that could lead to an answer.
Classical approach: regression analysis
Let’s again consider a linear model, for simplicity, using HGPA as our explanatory variable, in addition to C, an indicator variable for whether the student has had coaching. One concern is that only the more financially well-off families can afford coaching, so let’s use family income FI as another predictor. (We could of course consider some other factors as well, but let’s keep things simple.)
Our linear model then would be
E(S | HGPA, C, FI) = b0 + b1 HGPA + b2 C + b3 FI
where C is 1 or 0, depending on whether the student had coaching.
This would be the classical approach to assessing the effect of coaching. The quantity b2 represents the average extra points on the SAT, for students of fixed grades and family income. Comparing two students who are identical in grades and income, but one having the coaching and the other not, b2 is the expected difference in SAT. It would be the centerpiece of our analysis of the effects of coaching.
This is the traditional notion of ceteris paribus, “everything else being equal.” We might consider adding interaction terms (see below), but traditionally this would be the standard approach.
This model also allows one to investigate whether family income is a factor in SAT scores (directly, rather than though C). Studies on this have gone both ways, and my own analysis has suggested that the effect is small, but in any case, the above model could be used for such analysis.
What about interaction terms? Studies indicate that the higher-income kids are more likely to have been reading for pleasure since an early age. They thus have good reading comprehension and vocabulary, so the SAT coaching is not very useful to them. But the lower-income kids, perhaps reading less for pleasure, might benefit substantially from the coaching.
We would thus add an interaction term:
E(S | HGPA, C, FI) = b0 + b1 HGPA + b2 C + b3 FI + b4 C x FI
The above scenario would be reflected in an estimated value for b4 that is < 0 (assuming C > 0).
Note that now there is no single effect for the coaching, but rather one effect for each income level. A similar issue would arise if we forego a linear model, and turn to some nonparametric regression method, say kNN. This would involve estimating m(t) for various levels of t = (HGPA,C,FI) deemed of interest, and then comparing those estimates.
A causal approach: covariate matching
Note first, once again, that in the above linear model, it is NOT a problem if, say, our sample data skews toward higher incomes. As with any regression problem, we do have to consider sample size and assess linearity, but there is nothing inherently problematic about the skewed X distribution.
What saves us here? The answer is that we are taking covariates –HGPA and FI–into account. Raw comparison of SATs of the coached and noncoached groups could be very misleading in this setting, because the coached group might be richer and thus have, e.g., more experience reading for pleasure. It then would misleadingly look like the coaching led to higher SATs, rather than being due to differential backgrounds between the richer and poorer students.
Well, we can account for differences between covariates for the coached and noncoached groups in another way, by reconfiguring the data points in the two groups in such a way that the data is now balanced. Many ways have been devised for this, and a number of R packages have been developed along these lines.
For example, consider the function Matching::Match(y,treat,x). In our SAT example, y would be SAT, treat would be C, and x would be (HGPA,FI). The function forms pairs of students from the coached and noncoached groups, where in each pair the coached and noncoached students have the same or similar values of x. Those students who are selected (some may not be chosen) now give us two balanced groups, one coached and the other noncoached, who are similar in all respects other than coaching. For instance, the mean HGPA will be similar in the coached and noncoached groups, and so on. (After forming the groups, the pairing no longer is used.) We can now evaluate coaching fairly.
One drawback to covariate matching is that the larger the dimension of the X vector, the harder it is to do accurate covariate matching. An alternative is to match on just one summary quantity, the propensity score, which is the probability that the treatment will be “assigned.” In our SAT coaching example, it could be the probability that the student had coaching, given his/her family income. We can compute this using a logistic model, say, or a nonparametric technique such as kNN.
We then match on the propensity score alone; the third argument in Match would be that score, rather than the covariate vector X. The thinking is that by matching people with score 0.62, say, one of them who had coaching and one who didn’t, we’ve accounted for covariates.
A key point: the regression and matching approaches are fundamentally incomparable
Once again, the regression approach analyzes E(Y | X), a conditional mean, unaffected by the distribution of X. By contrast, covariate matching estimates E(Y), an unconditional mean, which is very strongly related to the distribution of X. If in the “family wealth” example above, the distribution of X is skewed toward the more well-off families, our analysis of the effect of coaching will be fair, but the magnitude of the effect will tell us how well coaching works among well-off families. Note that the same concern arises if the original distribution of X was not skewed but the data points that survive the selection process are skewed.
Directed Acyclic Graphs (DAGs):
Much of the surge in the use of causal analysis in recent years can be attributed to the attractiveness of DAGs; we all like pictures. Yet DAGs are a prime example of the importance of “knowing about something rather than just knowing the name of something.”
There are some extremely important points to keep in mind about DAGs. First, the word causal should not be taken literally; there is nothing in the framework about actual causation.
Second, DAGs cannot be generated by fitting from data; techniques for causal discovery require very strong assumptions. One can assess whether a DAG fits the data well, but not much more.
Third, DAGs are not unique. For any given set of probabilities, many different DAGs might fit those numbers equally well. Carnegie Mellon University statistics professor Cosma Shalizi has commented that it is highly misleading, indeed unethical, for a researcher to present a DAG without presenting other very different DAGs that are nevertheless mathematically equivalent.
Is causal analysis worth the extra trouble? Why not just use a linear regression model?
Linear models are very attractive here, easy to run and understand. One can add meaningful interaction terms, and if linearity is in question, we can try adding polynomial terms.
Another causal technique, structural equation models (SEMs), runs a series of regression models, in which not only is Y is expressed in the components of X, but also those components are expressed in terms of each other. Here again, we need not worry about skewing of distributions, providing we verify our linearity assumptions.
On the other hand, SEMs require that we have the DAG relating all the variables, and this cannot be determined from data; it essentially must be set from domain expertise in the field of study.
Why m(t)?
The above discussion regarding the irrelevance of whether X has a skewed distribution in some direction assumes that the quantity of interest is m(t) = E(Y | X=t), the regression function. Let’s take a closer look at this.
From a simple application of calculus, we know that the function f that minimizes the quantity E[(Y – f(X))2 | X = t] is m. So basically any prediction method that minimizes a sum of squares will take the form of a conditional mean. That includes linear models, of course, and also neural networks.
Note that the predicted value for a new case having X = t is the regression function value, m(t). Thus m is optimal in the sense of minimizing Mean Squared Prediction Error (at the population level).
Some predictive methods directly estimate m(t), such as k-NN and random forests.
What about predicting a dichotomous Y? Code Y to be 1 or 0. Then m(t) reduces to P(Y = 1 | X=t), and one can predict 1 or 0 depending on whether this quantity is greater or less than 0.5. (Or use another threshold for unequal error costs.) It can be shown that in this way, m(t) minimizes Overall Misclassification Error.
What about L1 models, say quantile regression? Here we minimize
E(|Y – f(X)| | X = t),
which has the solution f(t) = conditional median of Y given X = t. Then the same arguments goes through as before.
E[|Y – f(X)| | X = t, X in A] = E[|Y – f(X)| | X = t]
for the same reasons as before.
The same analysis works for any nonnegative loss function.
Assessing linearity:
One way to visually assess linearity (I frown on hypothesis testing in general, especially Goodness of Fit testing) is to fit linear and parametric models, then plot the latter against the former. Here’s an example:
library(qeML)
data(mlb1)
mlb <- mlb1[,-1] # height, weight, age
# predict weight from height, age, first using kNN then # a linear model
knnout <- qeKNN(mlb,'Weight',holdout=NULL)
lmout <- qeLin(mlb,'Weight',holdout=NULL)
lmpreds <- predict(lmout,mlb[,-2])
plot(knnout$regests,lmpreds)
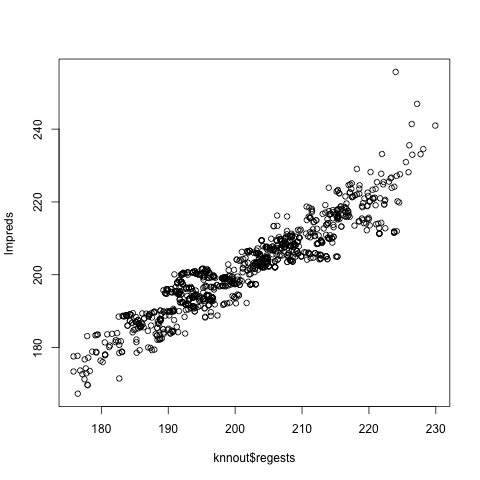
Looks pretty good overall, only a handful of outliers.